Survival Regression Models in PyMC

Time to Attrition in People Analytics

Nathaniel Forde

Data Science @ Personio

and Open Source Contributor @ PyMC

12/30/23

Agenda

  • Time to Event Distributions
    • HyperObjects and Perspectives on Probability
  • People Analytics and Survival Regression
    • Cox Proportional Hazard
    • Accelerated Failure Time
  • Comparing Model Implications
    • Marginal Predictions
    • Acceleration Factors
  • Frailty Models and Stratified Risk
  • Conclusion

The Pitch

Time to event data is everywhere. Understanding the temporal dynamics of event risk is crucial to management of organisational efficiency and costs.

The different flavours of complex hierarchical survival are all cleanly modelled as probabilities of state-transition within PyMC

Time to Event Distributions

Layered Abstractions and Hyperobjects

Concepts that defy easy panoptic survey prohibit easy action e.g. climate change and mathematical structures such as families of probability distributions

Perspectives on Probability

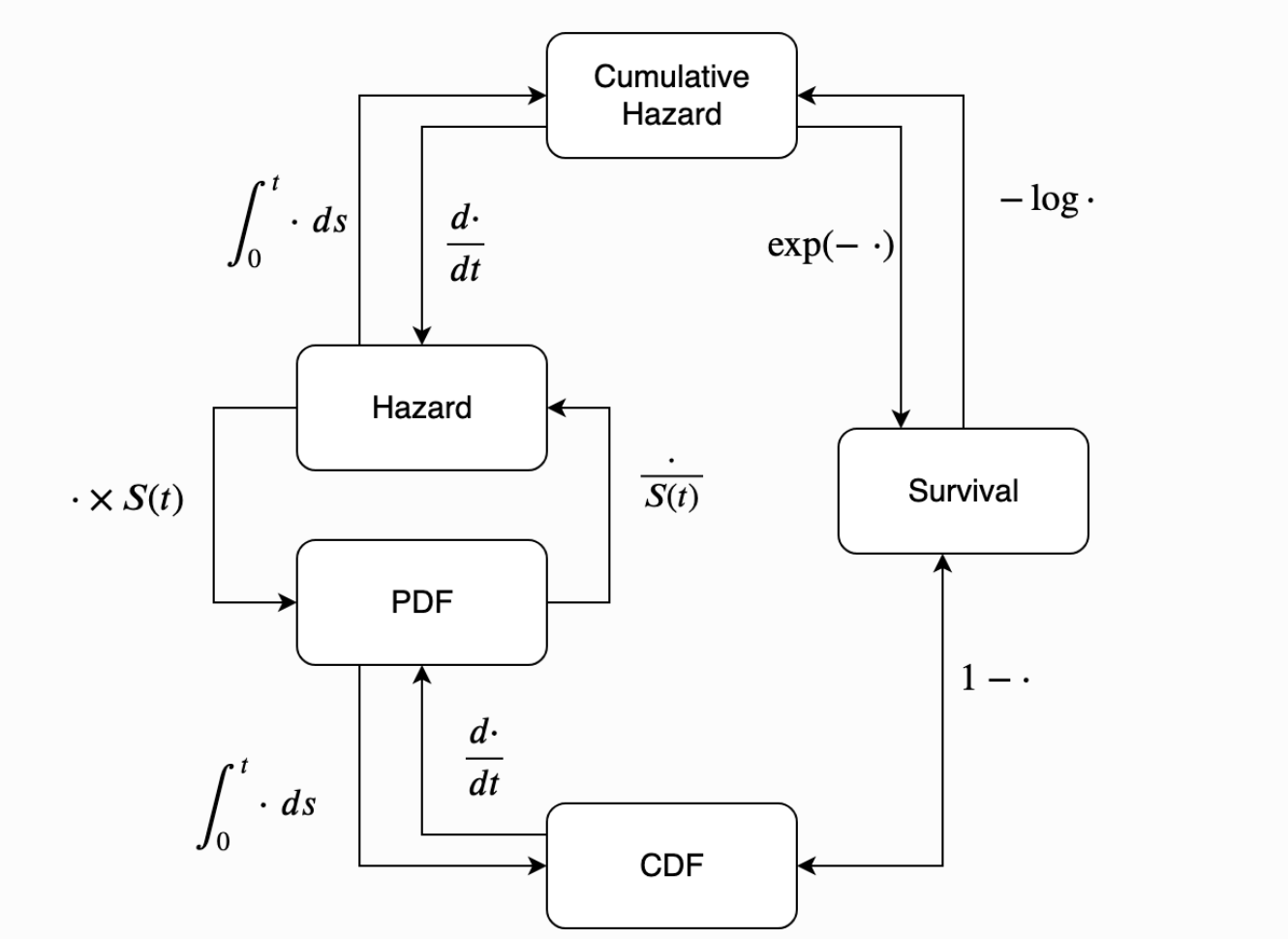
Top-Down and Abstract

Parametric CDF and Survival functions obscure views of instantaneous hazard

\[ h(t) = \frac{f(t)}{S(t)} \\ H(t) = -ln(S(t))\]

Baseline Instantenous Hazard

Actuarial Tables and Survival Curves

Bottom-Up and Concrete

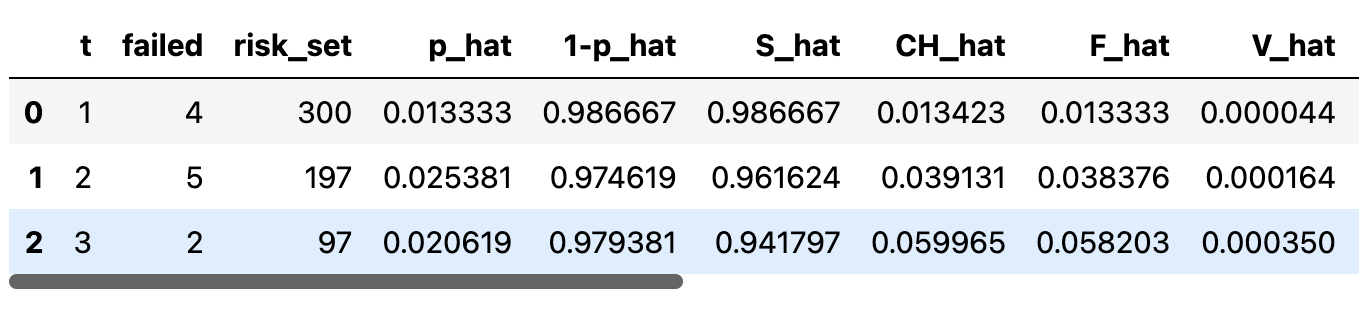
Actuarial Tables try to estimate CDF and Survival functions

Calculation of these abstract quantities proceeds from a clear and concrete notion of the risk-set in time.

Actuarial Tables and Survival Curves

Bottom-Up and Concrete

def make_actuarial_table(actuarial_table):
    ### Actuarial lifetables are used to describe the nature 
    ### of the risk over time derived from instantaneous hazard
    actuarial_table["p_hat"] = (actuarial_table["failed"] / 
                                actuarial_table["risk_set"])
    actuarial_table["1-p_hat"] = 1 - actuarial_table["p_hat"]
    ### Estimate of Survival function
    actuarial_table["S_hat"] = actuarial_table["1-p_hat"].cumprod()
    actuarial_table["CH_hat"] = -np.log(actuarial_table["S_hat"])
    ### The Estimate of the CDF function
    actuarial_table["F_hat"] = 1 - actuarial_table["S_hat"]
    actuarial_table["V_hat"] = greenwood_variance(actuarial_table)
    return actuarial_table

People Analytics and Survival Regression

Time to Attrition Data

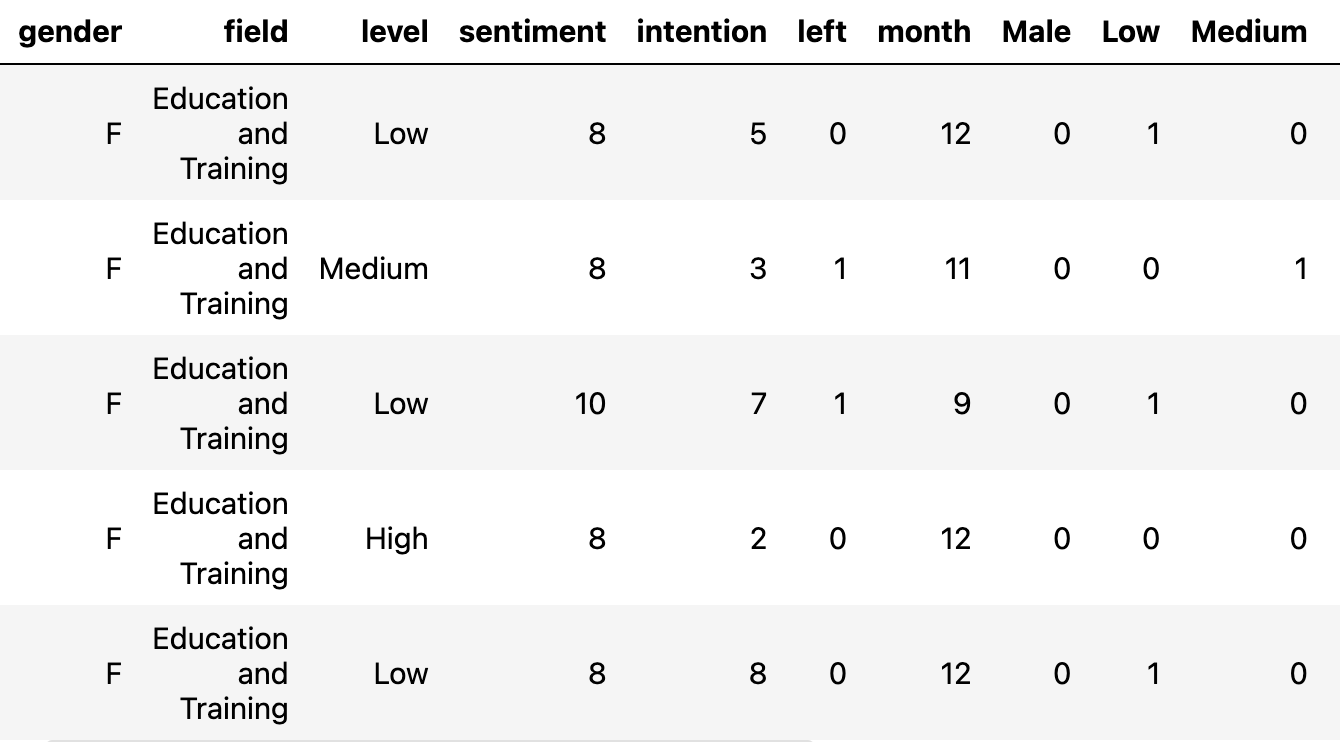Question: What is the relationship between individual characteristics and their expected survival times?

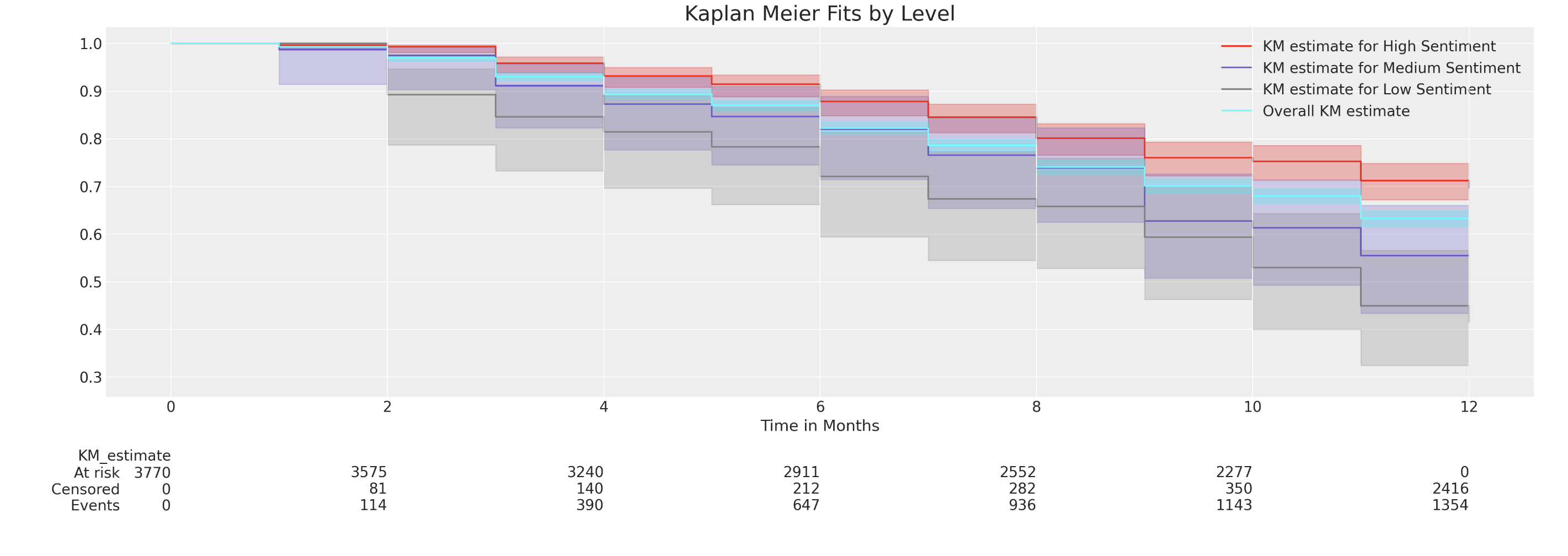
Question: How do individual survival times vary as a function of the levels in their covariates.

Regression and Censored Data

Censored Data Biases simple summaries

\[\mathbf{y_{i}} = \beta \mathbf{X_{i}} \]

\[\begin{split} \begin{pmatrix} \color{red}{y_{i, c}} \\ \color{blue}{y_{i, \neg c}} \\ \end{pmatrix} = \begin{pmatrix} \beta_{1} \\ \beta_{2} \\ \beta_{3} \end{pmatrix} \begin{pmatrix} \color{red}{x_{1,c}^{i}} & \color{red}{x_{2, c}^{i}} & \color{red}{x_{3, c}^{i}} \\ \color{blue}{x_{1,\neg c}^{i}} & \color{blue}{x_{2, \neg c}^{i}} & \color{blue}{x_{3, \neg c}^{i}} \\ \end{pmatrix} \end{split} \]

\[ \Rightarrow L(\mathbf{\beta}, S(\color{red}{y_{c}}), f(\color{blue}{y_{\neg c}}) ) \]

\[ \underbrace{p( \beta | y)}_{\text{posterior draws}} = \frac{p(\mathbb{\beta})L(\mathbf{\beta}, S(\color{red}{y_{c}}), f(\color{blue}{y_{\neg c}}) )}{\int_{i}^{n} L(\mathbf{\beta}_{i}, S(\color{red}{y_{c}}), f(\color{blue}{y_{\neg c}}) )p(\mathbf{\beta_{i}}) } \]

Regression for Survival Times

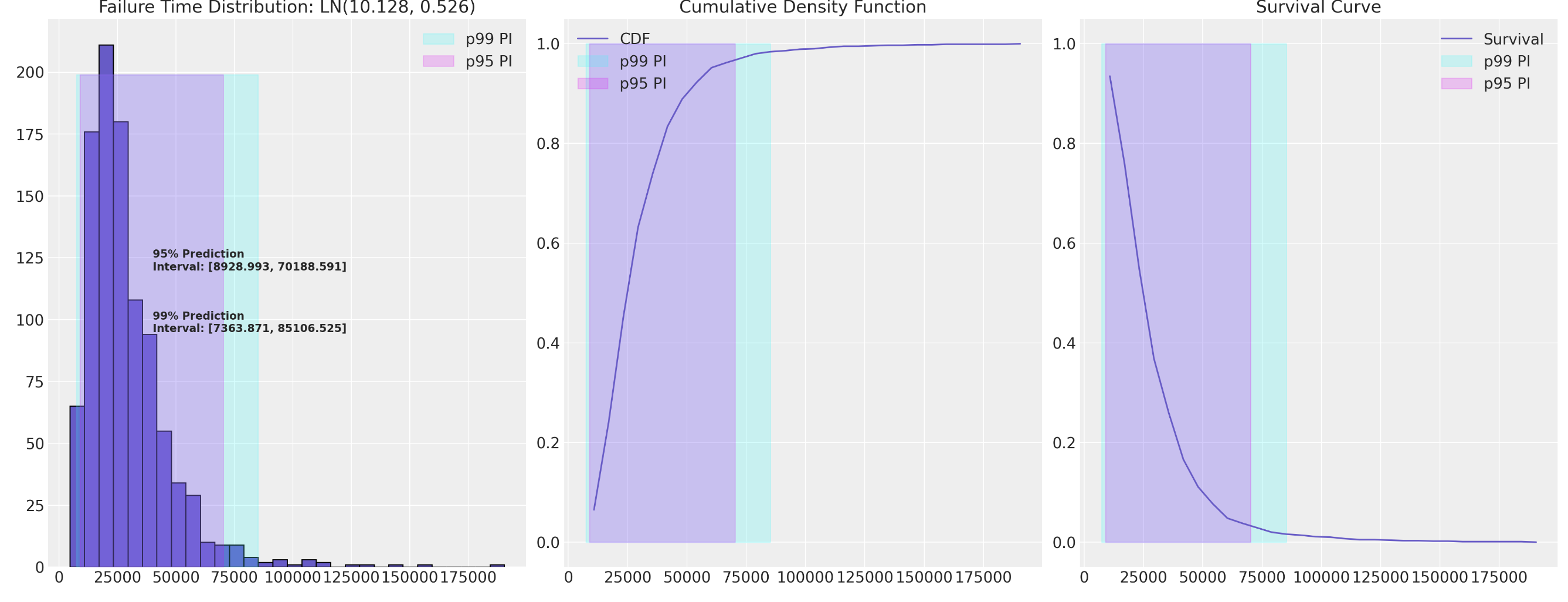
Distributions for Modelling Attrition

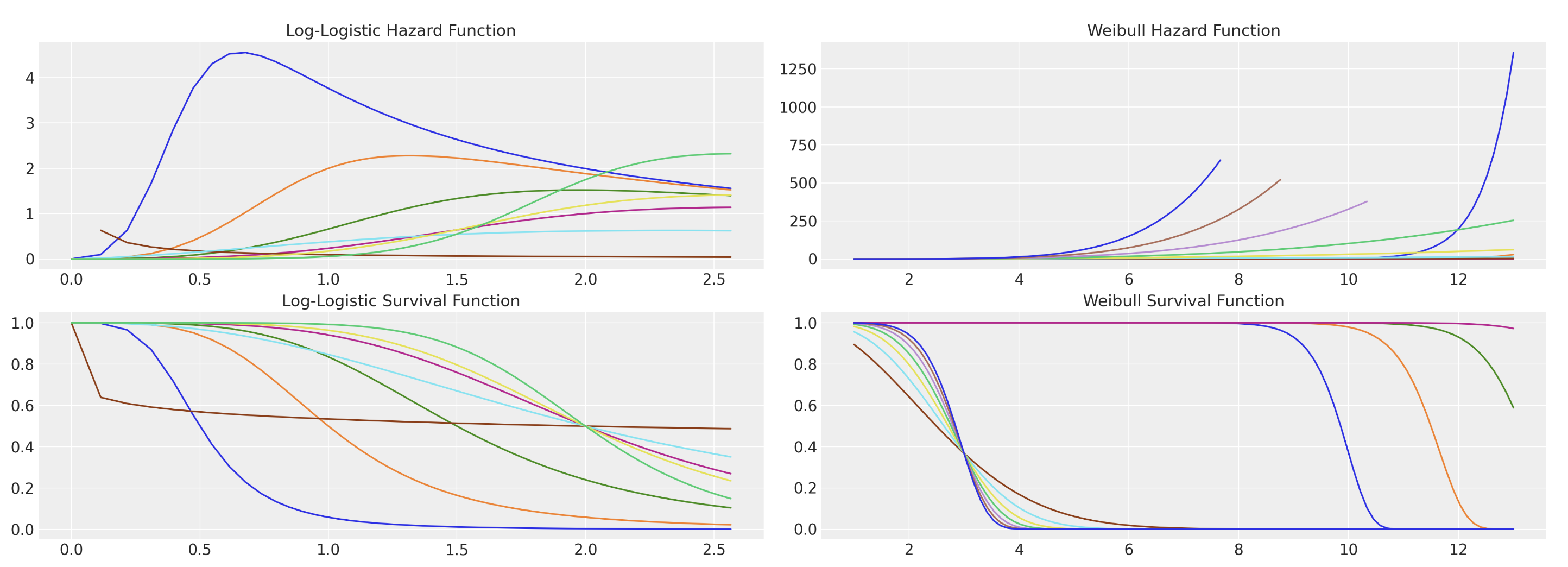
Monotonoc or non-monotonic hazards determined by distribution choice. Risk spikes important in early periods of employment.

Accelerated Failure Time Models

Parametric Models of Survival Distributions

\[S_{i}(t) = S_{0}\Bigg(\frac{t}{exp(\mu + \alpha_{1}x_{1} + \alpha_{2}x_{2} ... \alpha_{p}x_{p})} \Bigg) \]

with pm.Model(coords=coords, check_bounds=False) as aft_model:
  X_data = pm.MutableData("X_data_obs", X)
  beta = pm.Normal("beta", 0.0, 1, dims="preds")
  mu = pm.Normal("mu", 0, 1)

  s = pm.HalfNormal("s", 5.0)
  eta = pm.Deterministic("eta", pm.math.dot(beta, X_data.T))
  reg = pm.Deterministic("reg", pt.exp(-(mu + eta) / s))
  y_obs = pm.Weibull("y_obs", beta=reg[~cens], alpha=s, observed=y[~cens])
  y_cens = pm.Potential("y_cens", weibull_lccdf(y[cens], alpha=s, beta=reg[cens]))
  
  idata = pm.sample_prior_predictive()
  idata.extend(
      pm.sample(target_accept=0.95, random_seed=100, idata_kwargs={"log_likelihood": True})
  )
  idata.extend(pm.sample_posterior_predictive(idata))

Parametric Model Structure

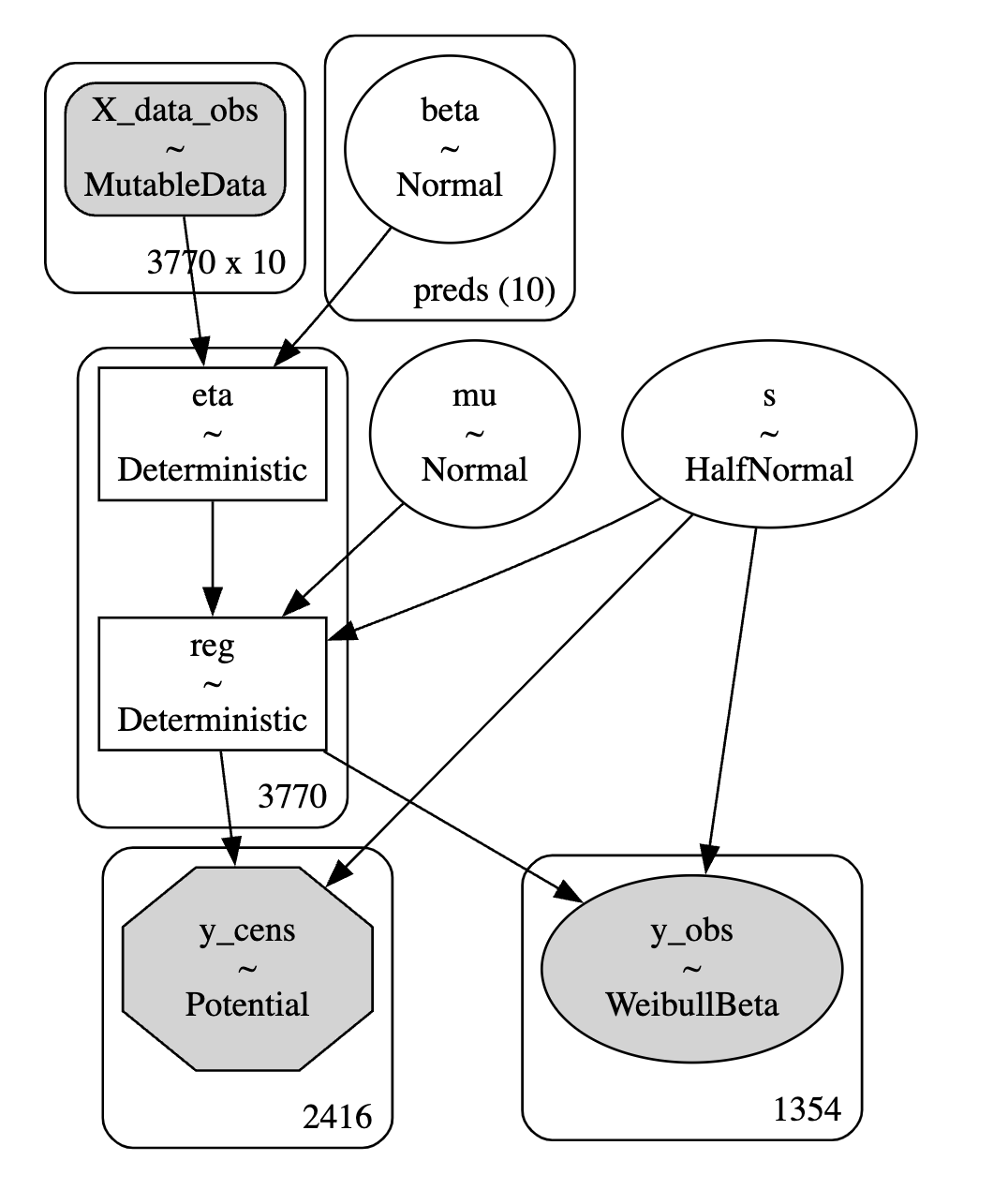
Accelerated Failure time models incorporate the regression component as a weighted sum that enters the parametric probability model

For instance: \[ Weibull(\alpha, \beta) \\ = Weibull(\alpha, reg)\]

Proportional Hazards Cox Regression

Flexible Discrete Intervals Hazards

\[ \text{Baseline Hazard: } \lambda_{0}(t) \] \[ \lambda_{0}(t) \cdot exp(\beta_{1}X_{1} + \beta_{2}X_{2}... \beta_{k}X_{k}) \]


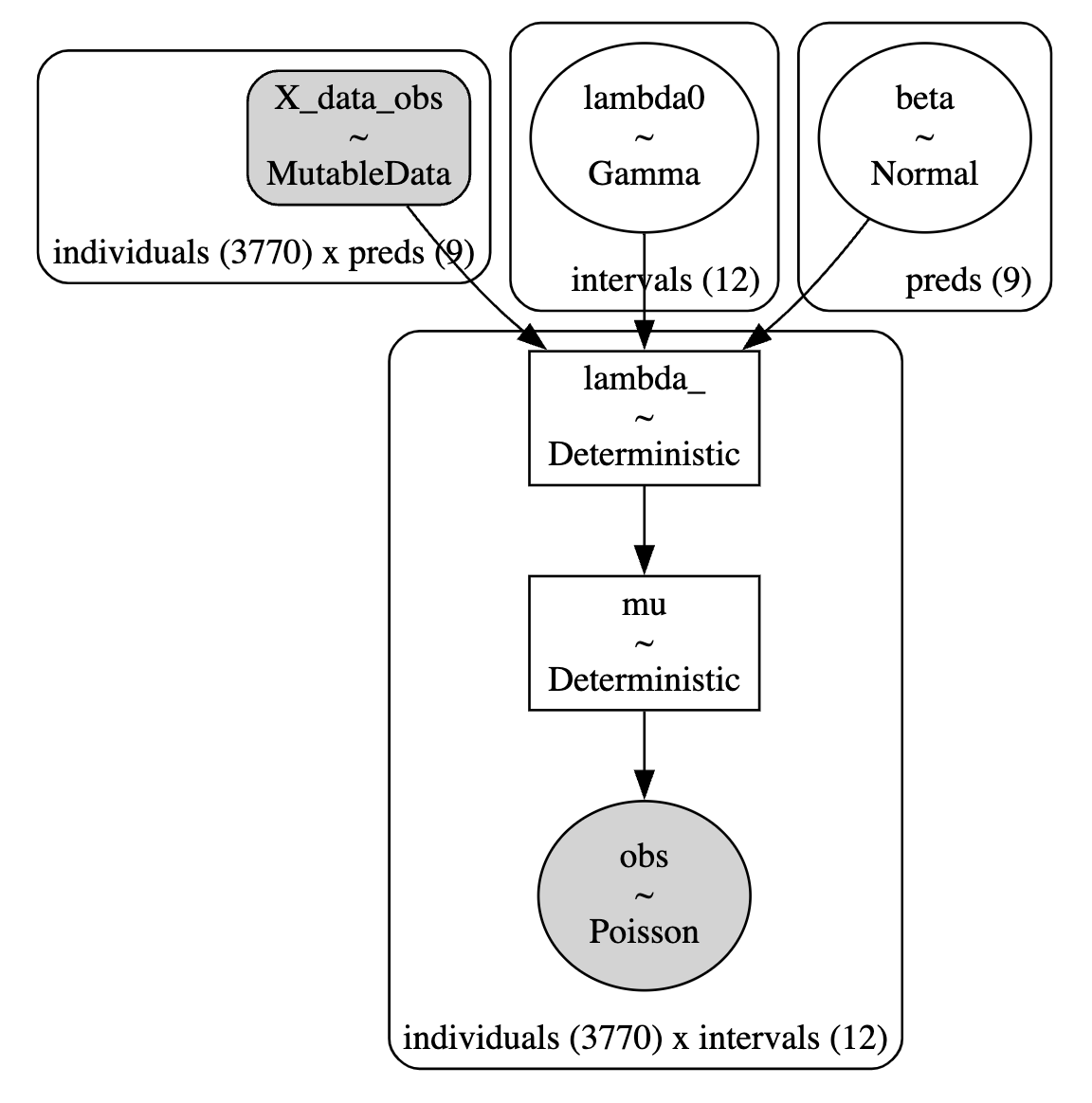
with pm.Model(coords=coords) as base_model:
  X_data = pm.MutableData("X_data_obs", retention_df[preds], dims=("individuals", "preds"))
  lambda0 = pm.Gamma("lambda0", 0.01, 0.01, dims="intervals")

  beta = pm.Normal("beta", 0, sigma=1, dims="preds")
  lambda_ = pm.Deterministic(
      "lambda_",
      pt.outer(pt.exp(pm.math.dot(beta, X_data.T)), lambda0),
      dims=("individuals", "intervals"),
  )
  mu = pm.Deterministic("mu", exposure * lambda_, 
                        dims=("individuals", "intervals"))

  obs = pm.Poisson("obs", mu, observed=quit, 
                    dims=("individuals", "intervals"))
  idata = pm.sample(
      target_accept=0.95, random_seed=100, idata_kwargs={"log_likelihood": True}
  )

Proportional Hazards Cox Regression

Sorites Paradoxes and accumulation of a triggering resource

“There’s the ‘mañana paradox’: the unwelcome task which needs to be done, but it’s always a matter of indifference whether it’s done today or tomorrow; the dieter’s paradox: I don’t care at all about the difference to my weight one chocolate will make.” - Dorothy Edgington

Baseline Instantenous Hazard

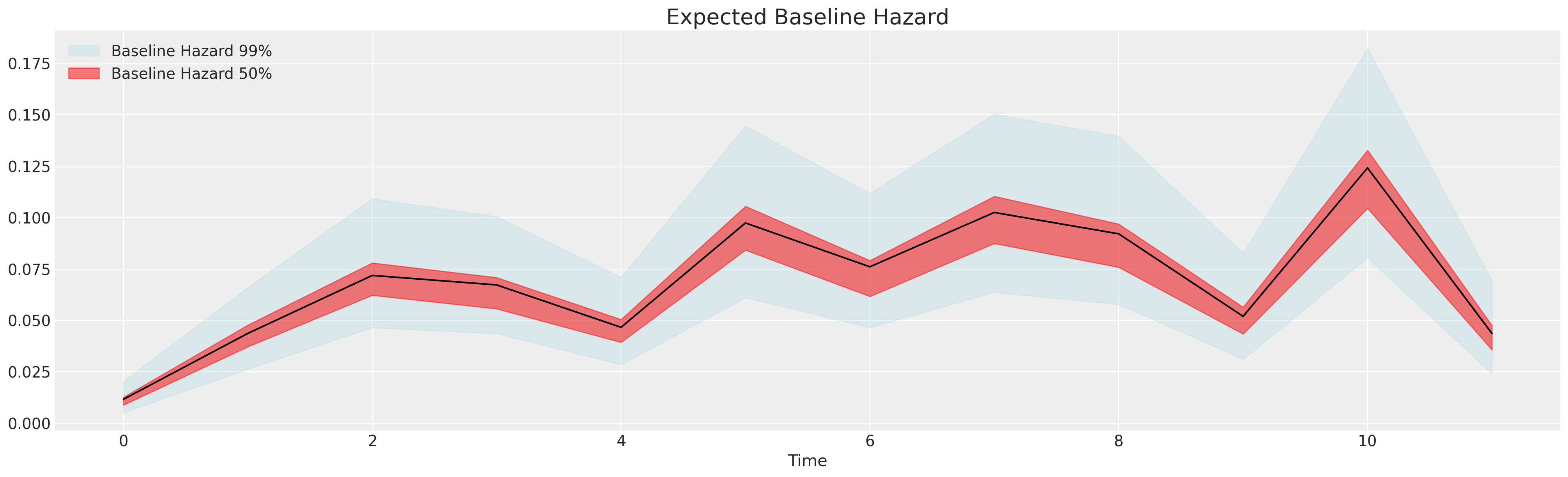
Proportional Hazards Cox Regression

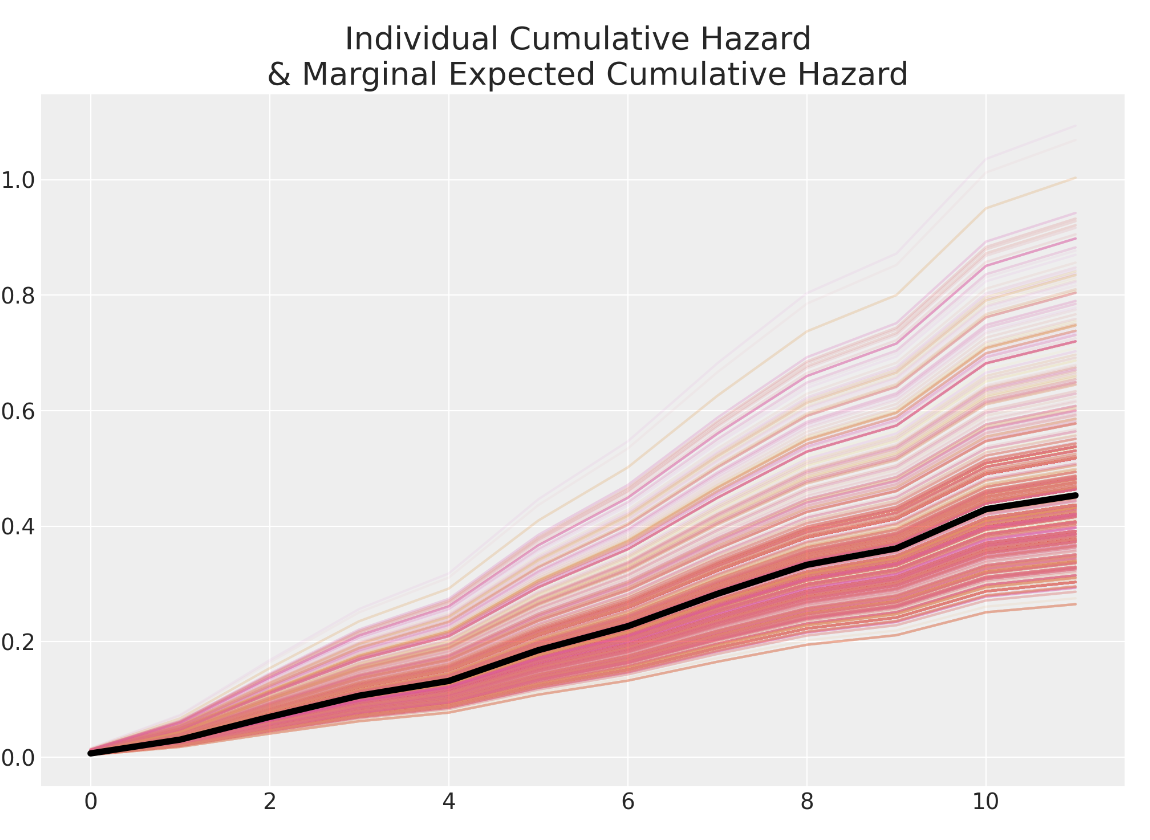
Cumulative Hazard across Individuals

Proportional Hazards Cox Regression

Using the Poisson Trick

\[ CoxPH(left, month) \sim gender + level \]

is akin to

\[ left \sim glm(gender + level + (1 | month)) \\ \text{ where link is } Poisson \]

applying an offset to the event rate for each time interval.

Proportional Hazards Cox Regression

The Proportional Hazards Assumption

  • The covariates enter once into the weighted sum that modifies the baseline hazard.
  • While the baseline hazard can change over time the difference in hazard induced by different levels in the covariates remains constant over time.

\[ \forall t \in T: \frac{h(t | X_{gender} = 1)}{h(t | X_{gender} = 0)} = constant \]

Comparing Model Implications

Comparing Models

Stated Intention and Sentiment

\[ CoxPH(left, month) \sim gender + field + level + sentiment \]

\[ CoxPH(left, month) \sim gender + field + level + sentiment + intention \]

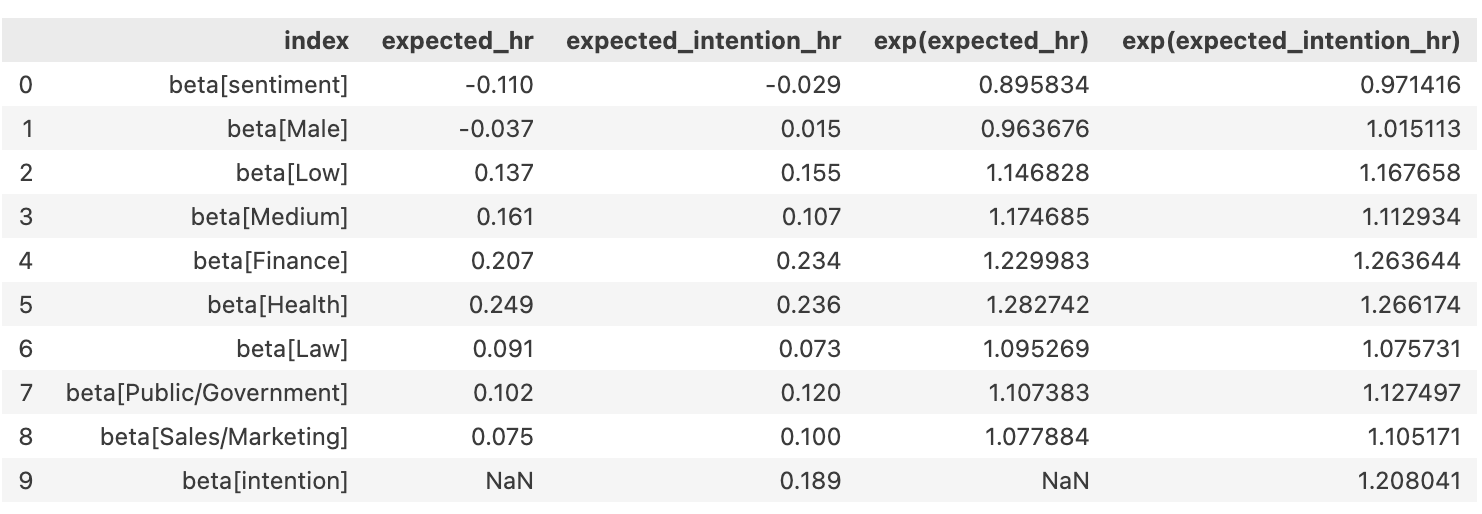
Comparing Models

Interpreting Model Coefficients

  • If \(exp(\beta)\) > 1: An increase in X is associated with an increased hazard (risk) of the event occurring.
  • If \(exp(\beta)\) < 1: An increase in X is associated with a decreased hazard (lower risk) of the event occurring.
  • If \(exp(\beta)\) = 1: X has no effect on the hazard rate.

Predicting Marginal Effects

Comparing Models

Predicting Marginal Effects

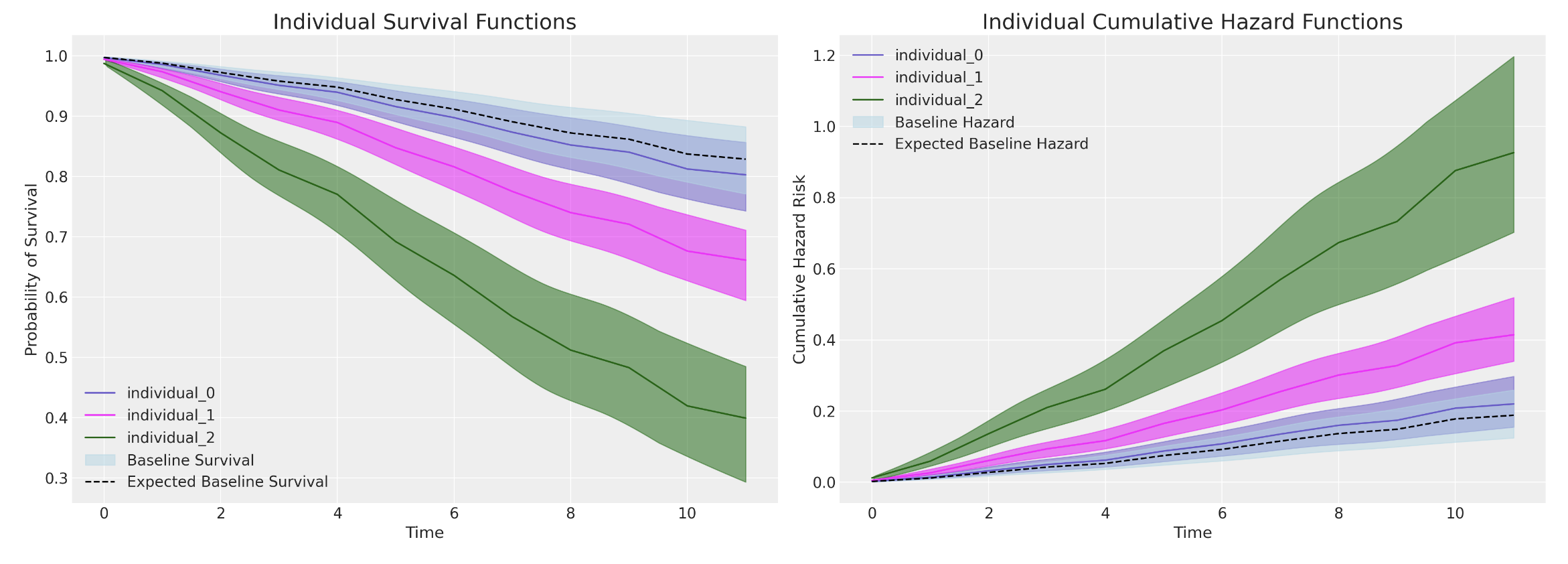
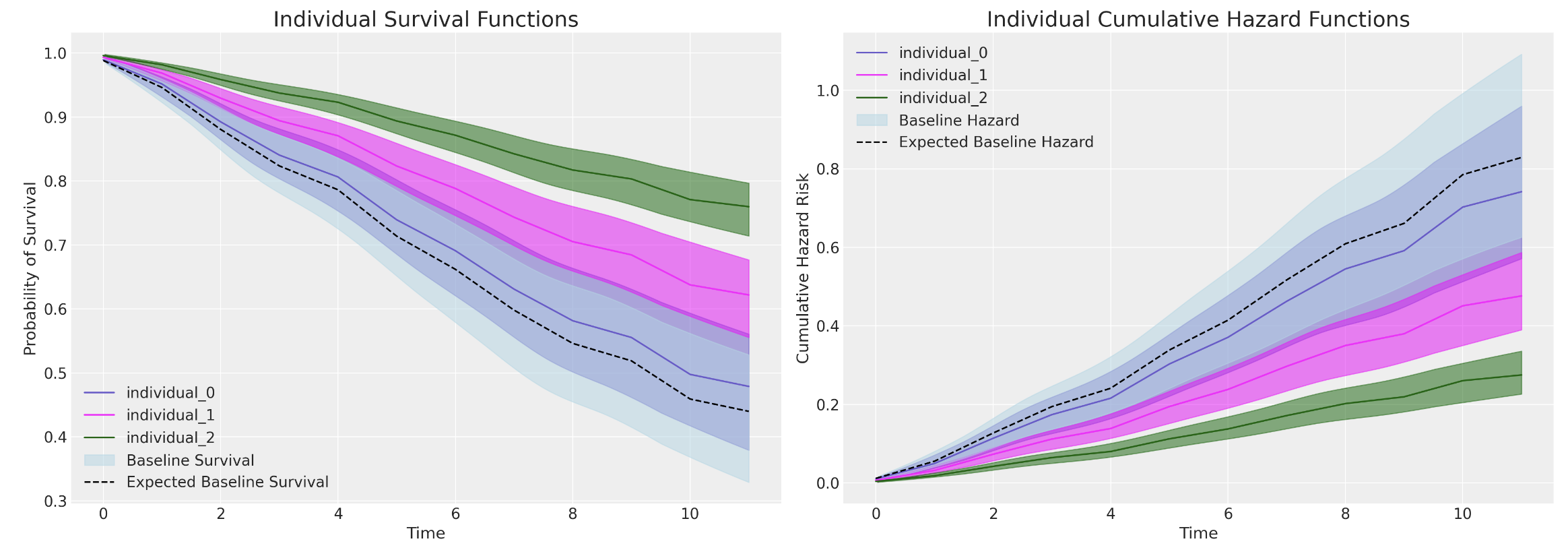
The Intention Model absorbs some of the variance in the baseline hazard not accounted for in the sentiment model

The Sentiment Model

Comparing Models

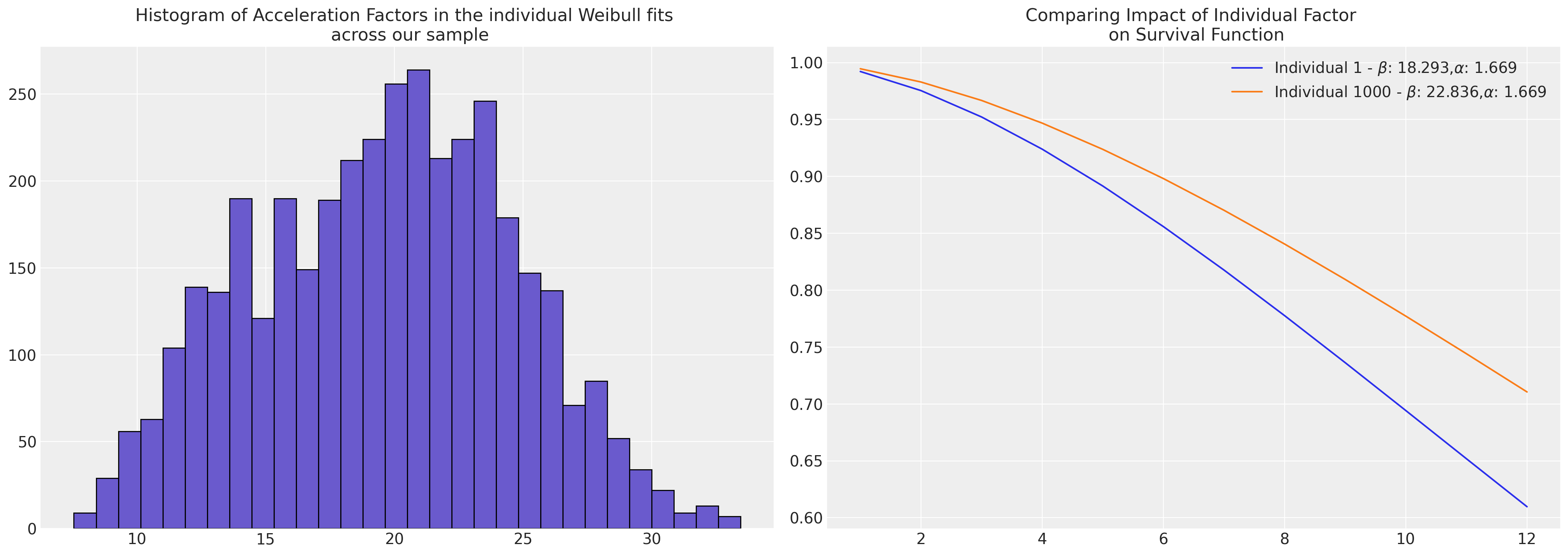
AFT models allow us to quantify the acceleration factor due to an individual or group’s risk profile.

Comparing Models

Marginal Survival Functions and WAIC

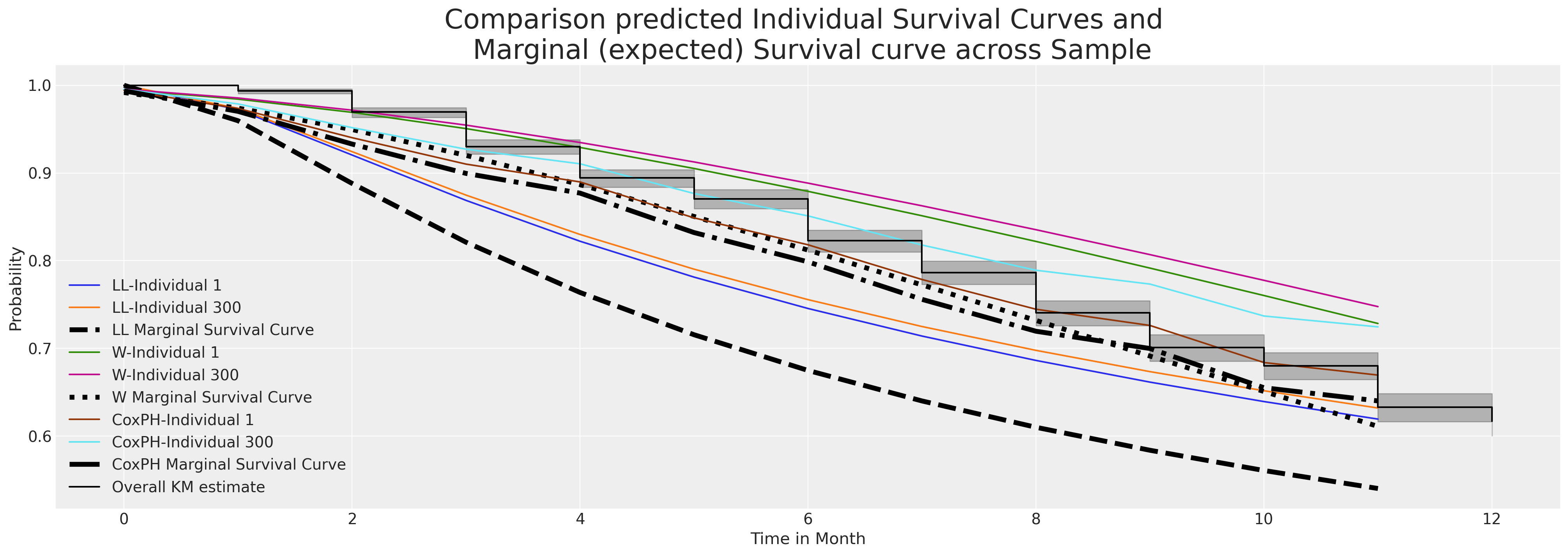
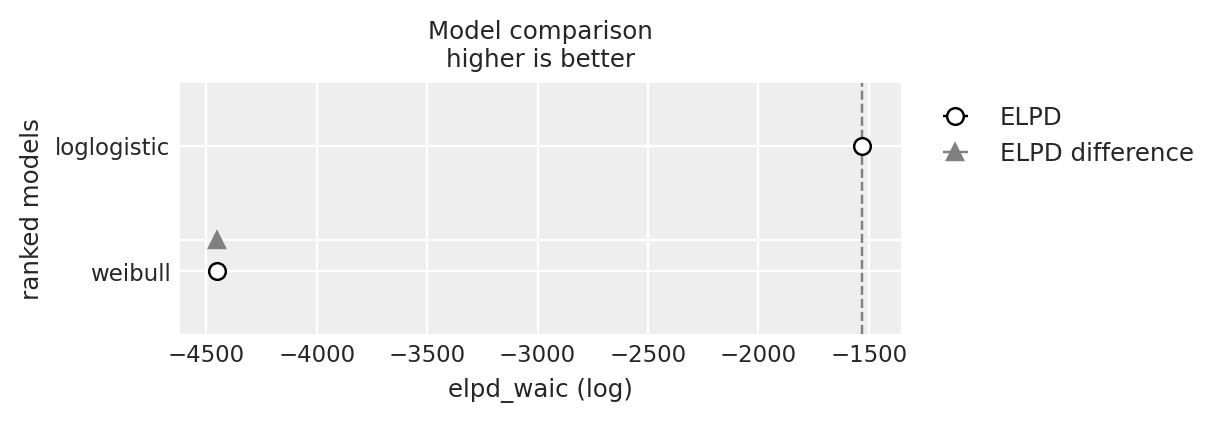
Comparing Marginal Survival Functions

Frailty Models and Stratified Risks

Frailty Models and Individual Heterogeneity

We want to relax the assumptions of Cox Proportional Hazards model. We introduce (i) frailty terms and (ii) stratified risks

\[ \lambda_{i}(t) = \color{green}{z_{i}}exp(\beta X)\color{red}{\lambda_{0}^{g}(t)} \]

The multiplicative frailty terms \(z_{i}\) can be specified as a gamma distribution centred on unity with stratified risks

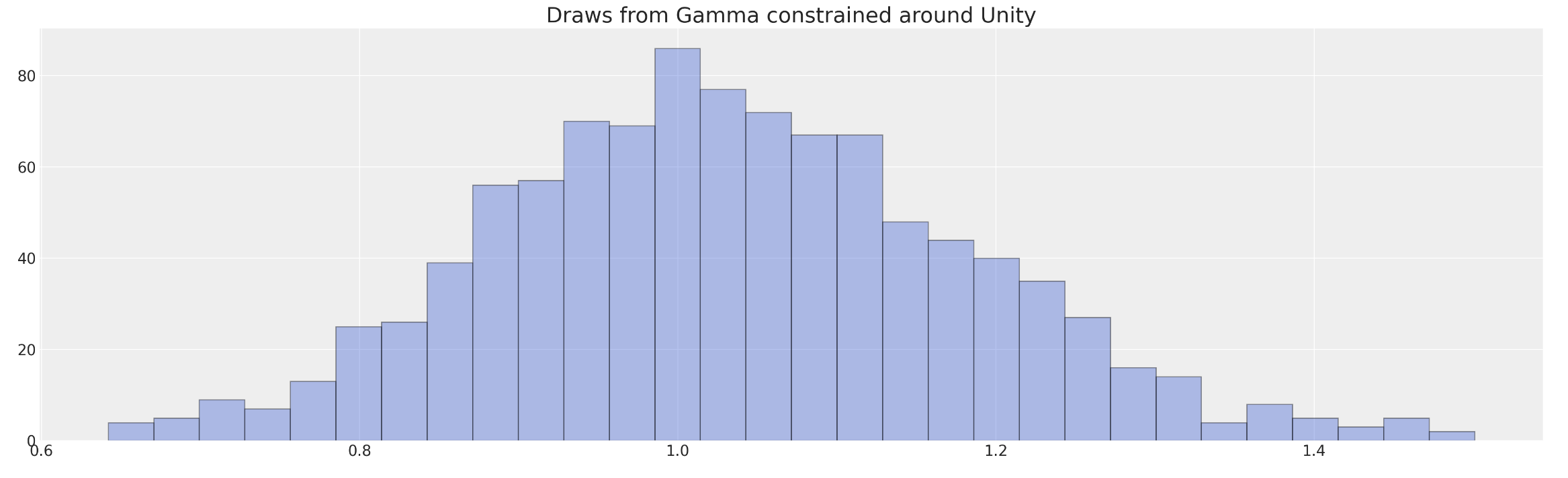
Frailty Model in Codes


with pm.Model(coords=coords) as frailty_model:
        X_data_m = pm.MutableData("X_data_m", df_m[preds], dims=("men", "preds"))
        X_data_f = pm.MutableData("X_data_f", df_f[preds], dims=("women", "preds"))
        lambda0 = pm.Gamma("lambda0", 0.01, 0.01, dims=("intervals", "gender"))
        sigma_frailty = pm.Normal("sigma_frailty", opt_params["alpha"], 1)
        mu_frailty = pm.Normal("mu_frailty", opt_params["beta"], 1)
        frailty = pm.Gamma("frailty", mu_frailty, sigma_frailty, dims="frailty_id")

        beta = pm.Normal("beta", 0, sigma=1, dims="preds")

        ## Stratified baseline hazards
        lambda_m = pm.Deterministic(
            "lambda_m",
            pt.outer(pt.exp(pm.math.dot(beta, X_data_m.T)), lambda0[:, 0]),
            dims=("men", "intervals"),
        )
        lambda_f = pm.Deterministic(
            "lambda_f",
            pt.outer(pt.exp(pm.math.dot(beta, X_data_f.T)), lambda0[:, 1]),
            dims=("women", "intervals"),
        )
        lambda_ = pm.Deterministic(
            "lambda_",
            frailty[frailty_idx, None] * pt.concatenate([lambda_f, lambda_m], axis=0),
            dims=("obs", "intervals"),
        )

        mu = pm.Deterministic("mu", exposure * lambda_, dims=("obs", "intervals"))

        obs = pm.Poisson("outcome", mu, observed=quit, dims=("obs", "intervals"))
        frailty_idata = pm.sample_prior_predictive()
        frailty_idata.extend(pm.sample(random_seed=101))

Frailty Model Structure

Individual Frailties

Frailty Model Structure

Shared Frailties

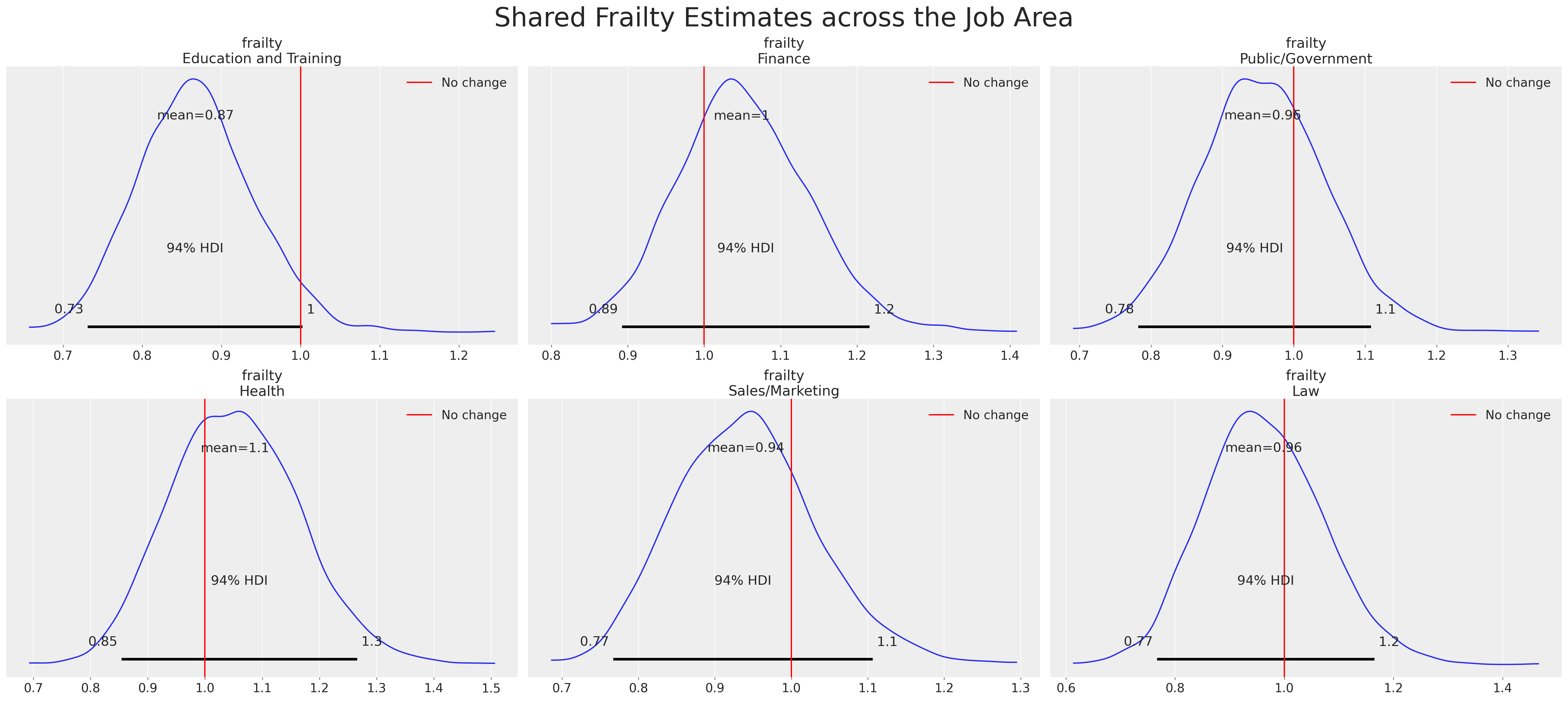
Shared Frailties by Field of Occupation

Frailty Models and Stratified Baseline Risks

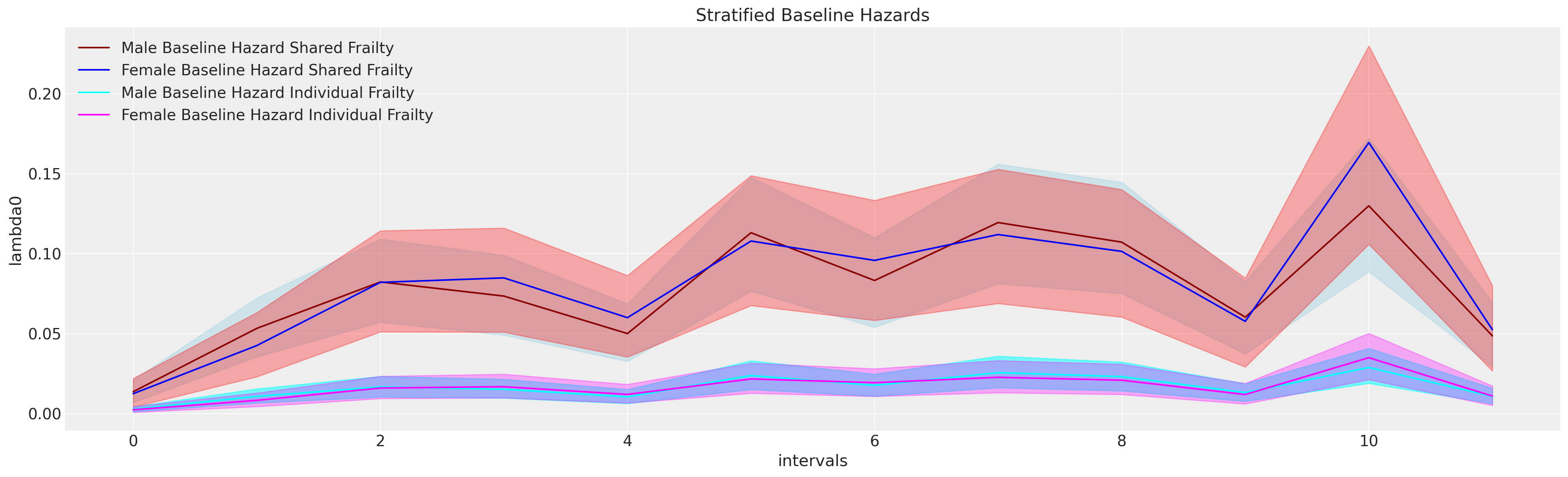
We see differences in the risks stratified by gender and additionally how the magnitude of the baseline hazard shrinks with more or less well-specified covariate in the model.

Individual Frailties and Marginal Statistics

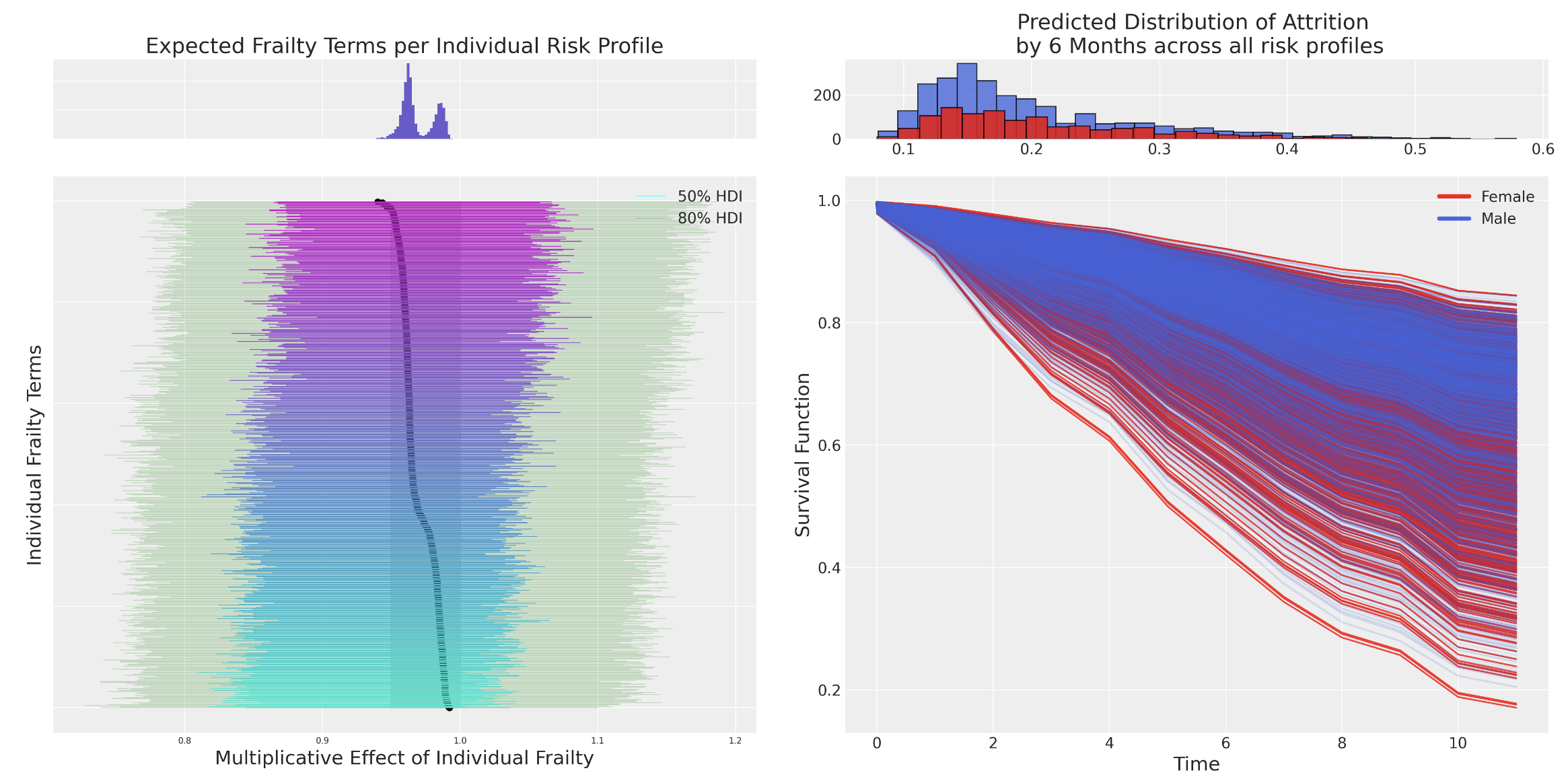
Conclusion

  • Survival Analysis is a tool for the expression of probabilities governing state-transitions
  • Important everywhere process efficiency and transformative outcomes matter. Corrects for censorship bias of naive summaries.
  • Allows for sophisticated expression of risk over time and along many dimensions. Variety of hierarchical modelling options
  • Bayesian estimation of these complex model structures is natural and informative. Meaningful across a range of disciplines and domains.
  • Provides an actionable lens on “actuarial” risk and “diagnostic” causal analysis in time.

Dicing with Death

When sand becomes a heap? When a heap returns to sand?

Survival Regression in PyMC